Home >> seismic load

Tag Archives: seismic load

I Simply Can’t Make the Numbers Work

I Simply Can’t Make the Numbers Work

Reader and Registered Professional Engineer LILA in LaCENTER writes:

“Is it possible to build a 56×66 pole structure with 4.5×5.5 laminated posts, 10 feet tall at 12′ centers with 110 mph winds in zone C and in seismic zone D? I would dearly love to see the numbers on this since my client insists it can be done based on Hansen’s assurances. I simply can’t make the numbers work.”

It is always a pleasure to work with Registered Professional Engineers, who may not design post-frame buildings on a regular basis. Here are “the numbers”:

COLUMN CALCULATIONS
Sidewall Columns
The following calculations assume a 3-ply 2×6 glu-lam SYP 2400f.

Step 1: Calculate the roof diaphragm stiffness, ch

Aside from panel end fasteners, panel length is proportional to the number of fasteners when the pattern of sheet-to-purlin fasteners in the diaphragm is maintained for the predicted building diaphragm
C1: stiffness of test panel
C1 = 0.5 × P / Ds × a / b ASAE EP 484.1, Eqn. 4 referenced in Design of Commercial Post-Frame Buildings p.44
for a simple beam test where
P: panel strength
P = Pultimate × 0.4
Pultimate: ultimate panel strength
Pultimate = 6600 lbs Townsend, p.4
P = 6600 lbs × 0.4
P = 2640 lbs
Ds: deflection at P adjusted for sinking supports
Ds = 0.265″ Townsend, p.4
a: test panel frame spacing
a = 144″ Townsend, p.4
b: test panel length parallel-to-corrugations
b = 140″ Townsend, p.4
C1 = 0.5 × 2640 lbs / 0.265″ × 144″ / 140″
C1 = 5123.45 lbs/in.
The roof diaphragm stiffness of a gable roof comprised of two equal slopes, ch, is given by:
ch = 2 × C1 × (b’ / b) × (a / sf) × cos2θ (Design of Commercial Post Frame Buildings, p.44)
ch = 2 × 5123.45 lbs/in × (366.824″ / 140″) × (144″ / 144″) × cos2(18.435)
ch = 24163.786 lbs/in

Step 2: Calculate the frame stiffness, k

k: frame stiffness
k = 6 × E’ × I / (H12 × (0.7 × d + h)) Skaggs Eqn. 1
E: modulus of elasticity
E’ = E × Ci
Ci: incising factor
Ci = 1 NDS 4.3.8
E’ = 2000000 psi × 1
E’ = 2000000 psi
I: moment of inertia
I = 46.273 in.4
H1: Height of column above grade
H1: 120″
d: embedment depth
d = 30″
k = 6 × 2000000 psi × 46.273 in.4 / (120″2 × (0.7 × 30″ + 120″))
k = 273.479lbs/in.

Step 3: Calculate the potential lateral restraining force of the roof diaphragm, R

R: lateral restraining force
R = |sf × (H1′ × (qWW – qLW) × (2.8 × d + 3 × H1) / (8 × (0.7 × d + H1)) + H2 × (qWR – qLR))| Skaggs Eqn. 2
H1′: Height of column above grade that experiences wind pressure
H1′ = 120″
R = |144″ × (120″ × (7.53 psf – -13.325 psf) / 144 psi/psf × (2.8 × 30″ + 3 × 120″) / (8 × (0.7 × 30″ + 120″)) + 112″ × (-19.471 psf – -14.514 psf) / 144 psi/psf)|
R = 429.896 lbs

Step 4: Calculate the diaphragm factor, mD

mD: diaphragm factor
ratio of frame-to-roof stiffness = k / ch
ratio = 273.479 lbs/in. / 24163.786 lbs/in.
ratio = 0.011
# of frames = 7
mD = 0.95 Skaggs Table 1

Step 5: Calculate the shear at top of the windward post, V

V: shear at the top of post
V = 0.5 × (R × mD + sf × (h × (qWW + qLW) × (2.8 × d + 3 × h) / (8 × (0.7 × d + h))) – h2 × (qWR – qLR)) Skaggs Eqn. 3
V = 0.5 × (429.896 lbs × 0.95 + 144″ × (120″ × (7.53 psf + -13.325 psf) / 144 psi/psf × (2.8 × 30″ + 3 × 120″) / (8 × (0.7 × 30″ + 120″))) – 112″ × (-19.471 psf – -14.514 psf) / 144 psi/psf)
V = 344.904 lbs
Δ = V / k
Δ = 344.904 lbs / 273.479 lbs/inch
Δ = 1″

Step 6: Calculate the maximum post moments, M1 and M2

M1: moment at groundline
M1 = h × (V – ((sf × qWW × h) / 2)) Skaggs Eqn. 4
M1 = 120″ × (344.904 lbs – ((144″ × 7.53 psf / 144 psi/psf × 120″) / 2))
M1 = -12824.334 in.lbs
M2: moment above groundline
M2 = V2 / (2 × sf × qWW) Skaggs Eqn. 5
M2 = (344.904 lbs)2 / (2 × 144″ × 7.53 psf / 144 psi/psf)
M2 = 7899.459 in.lbs

Step 7: Calculate the axial compression force in post, Pf

Pf: compressive force post
Load Combinations (IBC):
1. D
Pf, D = sf × w / 2 × (roof dead load) + 0 × (H2 / (2 × w)) × (R × mD + sf × H2 × (qLR – qWR))
Pf, D = 144″ × 336″ × (15 psf / 144 psi/psf) + 0 lbs
Pf, D = 5040 lbs
2. D + S
Pf, D+S = sf × w / 2 × (roof dead load + roof snow load) + 0 × (H2 / (2 × w)) × (R × mD + sf × H2 × (qLR – qWR))
Pf, D+S = 144″ × 336″ × ((15 psf + 25 psf) / 144 psi/psf) + 0 lbs
Pf, D+S = 13440 lbs
3. D + W
Pf, D+W = sf × w / 2 × (roof dead load + (qWR – qLR)) + (H2 / (2 × w)) × (R × mD + sf × H2 × (qLR – qWR))
Pf, D+W = 144″ × 336″ × ((15 psf + (-19.471 psf – -14.514 psf)) / 144 psi/psf) + (112 / (2 × 672)) × (429.896 lbs × 0.95 + 144″ × 112″ ((-14.514 psf – -19.471 psf) / 144 psi/psf))
Pf, D+W = 3374.537 lbs
4. D + 0.75S + 0.75W
Pf, D+0.75S+0.75W = sf × w / 2 × (roof dead load + 0.75 × roof snow load + 0.75 × (qWR – qLR)) + 0.75 × (H2 / (2 × w)) × (R × mD + sf × H2 × (qLR – qWR))
Pf, D+0.75S+0.75W = 144″ × 336″ × ((15 psf + 0.75 × 25 psf + 0.75 × (-19.471 psf – -14.514 psf)) / 144 psi/psf) + 0.75 × (112 / (2 × 672)) × (429.896 lbs × 0.95 + 144″ × 112 ” ((-14.514 psf – -19.471 psf) / 144 psi/psf))
Pf, D+0.75S+0.75W = 10151.125 lbs

Step 8: Check post adequacy at groundline

CM: wet service factor
CM = 1 Column is protected from excessive moisture by building shell, concrete, or embedment
CD: load duration factor
CD = 1.6 NDS 2.3.2
Ci: incising factor
Ci = 1 NDS 4.3.8
CF: size factor
CF = 1 NDS Supplement
Ct: factor
Ct = 1 NDS 4.3
CP: column stability factor
CP = 1 NDS 3.7
Fc’: allowable compressive force post
Fc’ = Fc × CD × CM × Ct × CF × Ci × CP NDS 4.3
Fc’ = 1975 psi × 1.6 × 1 × 1 × 1 × 1 × 1
Fc’ = 3160 psi
CM = 1 Column is protected from excessive moisture by building shell, concrete, or embedment
Cr: repetitive member factor
Cr = 1 NDS 4.3
CF = 1 NDS Supplement
CL: beam stability factor
CL = 1 NDS 4.3
Cfu: flat use factor
Cfu = 1 NDS 4.3
Fb’: allowable bending stress post
Fb’ = Fb × CD × CM × Ct × CL × CF × Cfu × Ci × Cr NDS 4.3
Fb’ = 3000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb’ = 4800 psi
fc: axial compressive force post
fb: bending stress post
Load Combinations (IBC):
1. D
fc, D = Pf, D / (b × d)
fc, D = 5040 lbs / (21.141in2)
fc, D = 238.404 psi
fb, D = 0 × |M1| / S NDS 3.3.2
fb, D = 0 × |-12824.334 in.lbs| / 18.058 in3
fb, D = 0 psi
(fc, D / Fc’)2 + fb, D / Fb’ ≤ 1
(238.404 psi /3160psi)2 + 0 ≤ 1
0.006 ≤ 1
2. D + S
fc, D+S = Pf, D+S / (b × d)
fc, D+S = 13440 lbs / (21.141in2)
fc, D+S = 635.743 psi
fb, D+S = 0 × |M1| / S NDS 3.3.2
fb, D+S = 0 × |-12824.334 in.lbs| / 18.058 in3
fb, D+S = 0 psi
(fc, D+S / Fc’)2 + fb, D+S / Fb’ ≤ 1
(635.743 psi /3160psi)2 + 0 ≤ 1
0.04 ≤ 1
3. D + W
fc, D+W = Pf, D+W / (b × d)
fc, D+W = 3374.537 lbs / (21.141in2)
fc, D+W = 159.623 psi
fb, D+W = |M1| / S NDS 3.3.2
fb, D+W = |-12824.334 in.lbs| / 18.058 in3
fb, D+W = 710.19 psi
(fc, D+W / Fc’)2 + fb, D+W / Fb’ ≤ 1
(159.623 psi /3160psi)2 + 710.19 psi / 4800 psi ≤ 1
0.151 ≤ 1
4. D + 0.75S + 0.75W
fc, D+0.75S+0.75W = Pf, D+0.75S+0.75W / (b × d)
fc, D+0.75S+0.75W = 10151.125 lbs / (21.141in2)
fc, D+0.75S+0.75W = 480.171 psi
fb, D+0.75S+0.75W = 0.75 × |M1| / S NDS 3.3.2
fb, D+0.75S+0.75W = 0.75 × |-12824.334 in.lbs| / 18.058 in3
fb, D+0.75S+0.75W = 532.642 psi
(fc, D+0.75S+0.75W / Fc’)2 + fb, D+0.75S+0.75W / Fb’ ≤ 1
(480.171 psi /3160psi)2 + 532.642 psi / 4800 psi ≤ 1
0.134 ≤ 1
Column stressed to a maximum of 15.1%

Step 9: Check post adequacy at positive moment region

Fc’ = Fc* × CP NDS 4.3
CP: column stability factor
CP = (1 + (FcE / Fc*)) / (2 × c) – √(((1 + (FcE / Fc*)) / (2 × c))2 – (FcE / Fc*) / c) NDS 3.7.1
FcE = 0.822 × Emin’ / (le / d)2
Ke = 0.8 NDS 3.7.1
le = Ke × h NDS 3.7
le = 0.8 × 24″
le = 19.2″
FcE = 0.822 × 1020000 psi / (19.2″ / 5.125″)2
FcE = 59738.907 psi
CP = (1 + (59738.907 psi / 3160 psi)) / (2 × 0.9) – √(((1 + (59738.907 psi / 3160 psi)) / (2 × 0.9))2 – (59738.907 psi / 3160) / 0.9)
CP = 0.994
Fc’ = 3160 psi × 0.994
Fc’ = 3142.551 psi
fb: bending stress post

Load Combinations (IBC):

1. D
fb , D = 0 × M2 / S
fb , D = 0 × 7899.459 in.lbs / 18.058 in3
fb , D = 0 psi
(fc, D / Fc’)2 + fb, D / Fb’ ≤ 1
(238.404 psi /3142.551psi)2 + 0 ≤ 1
0.006 ≤ 1
2. D + S
fb, D+S = 0 × M2 / S
fb, D+S = 0 × 7899.459 in.lbs / 18.058 in3
fb, D+S = 0 psi
(fc, D+S / Fc’)2 + fb, D+S / Fb’ ≤ 1
(635.743 psi /3142.551psi)2 + 0 ≤ 1
0.041 ≤ 1
3. D + W
fb, D+W = M2 / S
fb, D+W = 7899.459 in.lbs / 18.058 in3
fb, D+W = 437.459 psi
(fc, D+W / Fc’)2 + fb, D+W /(Fb’ × (1 – fc, D+W / FcE)) ≤ 1
(159.623 psi /3142.551psi)2 + 437.459 psi / 4800 psi × (1 – 159.623 psi / 59738.907 psi)) ≤ 1
0.094 ≤ 1
4. D + 0.75W + 0.75S
fb, D+0.75S+0.75W = 0.75 × M2 / S
fb, D+0.75S+0.75W = 0.75 × 7899.459 in.lbs / 18.058 in3
fb, D+0.75S+0.75W = 328.094 psi
(fc, D+0.75S+0.75W / Fc’)2 + fb, D+0.75S+0.75W / Fb’ × (1 – fc, 0.75wind / FcE)) ≤ 1
(480.171 psi /3142.551psi)2 + 328.094 psi / 4800 psi × (1 – 480.171 psi / 59738.907 psi)) ≤ 1
0.092 ≤ 1
Column stressed to a maximum of 9.4%

∴ A 3-ply 2×6 glu-lam SYP 2400f column is adequate.

This entry was posted in Professional Engineer, Columns, Barndominium, Pole Barn Questions, Pole Barn Design, Building Department, Constructing a Pole Building, Pole Barn Structure and tagged seismic load, column stiffness, design load, frame stiffness, diaphragm factor, post frame design, wind load on February 6, 2025 by Rick Ochs.

Properly Treated Posts, Hillside Locations, and a Post Frame Option

This week the Pole Barn Guru answers questions about properly treated posts, building on hillside locations, and an option to build with post frame.

DEAR POLE BARN GURU: According to most of the answers on the Internet, if I bury the posts for my deck they will rot away and the whole thing will come crashing down 10 or so years. What proprietary space-age technology are you using in your pole barns that deck builders don’t know about?
(yes this is a bit tongue-in-cheek) MM in MILTON

DEAR MM: How about we start with over 50% of all builders did not graduate from high school? The great majority of deck builders call in, text or email the lumber list for the next deck to their supplier of choice. I worked in or owned my own lumber yards for years and never, ever can I recall a builder specifying a level of treatment when they ordered pressure preservative treated wood.

Builder says treated, and he gets treated….probably not adequate for most applications. Any lumber placed structurally into the ground should be treated to a minimum UC-4B retention. I wrote this article for Rural Builder magazine, so it is directed specifically towards builders and suppliers, however it should make my point: https://www.hansenpolebuildings.com/2014/05/building-code-3/.

DEAR POLE BARN GURU: I have a hillside location and am looking for information on pole housing in California and their seismic ratings? ROBIN in SAN DIMAS

DEAR ROBIN: San Dimas – the town Bill and Ted made famous! Post frame (pole) buildings perform admirably on hillsides, as they can be attached to partial foundations (https://www.hansenpolebuildings.com/2012/02/grade-change/) or built on stilts (https://www.hansenpolebuildings.com/2017/09/stilt-houses/) to compensate for grade changes.

As far as seismic design, structures are affected by earthquake in relationship to the weight of the structure. The lighter the structure, the more resistant it is to tremors! Here is a little earthquake reading: https://www.hansenpolebuildings.com/2015/10/a-whole-lotta-shakin-going-on/ and https://www.hansenpolebuildings.com/2016/05/earthquake-resistant-post-frame-construction/.

DEAR POLE BARN GURU: I am in the engineering phase of our forever home in Minnetonka. I have an architect drafting my designs, and am now working with structural engineers to figure out the best way to construct it. My original plans show double stud 2×4 walls (for super insulation), and our ceiling heights are on the tall side.

An option we are considering is getting the house pole framed for the interior stud wall, and then site framing the exterior stud wall, in order to create the cavity for super insulating. I also plan to use an interior ledger system for the floor joists.

Let me know if you think this is a possibility. I can send you our current drawings for you to look at. There are obviously a lot more details to sift through than what I’ve covered in this email.

Let me know! Thanks! SONJA in MINNETONKA

DEAR SONJA: One of the great features about investing in a post frame building kit package (at least from Hansen Pole Buildings) is it includes the engineered structural plans for your new home – no need to pay an expensive structural engineer!

Installing Drywall on Ceiling There is probably a much easier way to achieve your super insulated walls – using post frame construction and ‘commercial’ bookshelf style girts, you can create a deep wall insulation cavity for one or a combination of the following: unfaced fiberglass or rock wool (best since it is not effected by moisture) batts; BIBs (https://www.hansenpolebuildings.com/2011/11/bibs/); and/or closed cell spray foam. Between the inside of the framing and the wallboard, use high R insulation board, which creates a thermal break between and wall framing and the interior conditioned space.

We’d be pleased to assist you in your project.

This entry was posted in Insulation, Pole Barn Design, Columns, Pole Barn Homes and tagged UC-4B, post frame house, seismic load, super insulate, treated posts, hillside building on July 30, 2018 by admin.

Builders Who Make No Upgrades in Twenty-Five Years

Builders Who Make No Upgrades in Twenty-Five Years.

Why?

We’ve Been Building This Way for 25 Years
In the event you happen to hear this from a pole builder – run away from them as quickly as possible.
Why?
Because every three years there is a new version of the Building Codes and often those new Codes come with changes in the way wind, snow and or seismic loads are applied to the building. New methods and materials seem to appear on the market so fast they make one’s head spin. Technology moves at a breakneck speed and to be doing things exactly the same for 25 years means your proposed erector is pre-internet in thinking!!

COREY in BILLINGS writes:
“Good Morning,
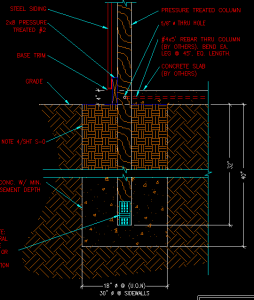I was speaking to Rachel and she gave me your email to see if you might be able to answer a question for me. I hired complete a 50’x 80’ x 12’ pole barn here in Huntley, MT. The company showed up on the job yesterday and drilled the holes and started setting posts. Posts are 8’ center. They set the corner posts and maybe 6 sidewall posts and 4 endwall posts. The other posts were placed in the drilled holes and left for completion today/tomorrow. When I inspected the posts that were placed but not set (no backfill) I noticed that there was no footing or no cleats attached to post base to prevent uplift. When I questioned the owner of the company what he was using for footings he stated nothing added just solid tamped. I immediately called him and questioned his reasoning and got the I have been building these like this for 25 years. My question is on average what is the post load in psi on the 50’ x 80’ x 12’ pole barn with a 40# snow load? My soil has a bearing capacity of 2100 psi.”
In my humble opinion, you need to stop them immediately. Just because they have been doing them this way for 25 years does not make it correct.

Mike the Pole Barn Guru Writes:

Assuming a 40# design roof snow load and minimal design dead loads (usually 3.3 psf top chord and 1 psf bottom chord) gives a total of 44.3 psf X 8′ on center X 50’/2 = 8860# downward If they are using 6×6 posts (5-1/2″ nominal) they are placing over 42,000 psf on the base of the column!!

Roughly 21 times the soil bearing capacity.

Each post should probably have a concrete pad 30 inches or so in diameter underneath and at least 6 (if not 8) inches thick.

If I were you, I’d be requiring the building contractor to submit engineer sealed plans for your building to you (even if you have to pay for the cost). Otherwise you are pretty well hung out to dry.