How Far Can a 2×6 Purlin Span?
Reader WILL in COMFORT writes:
“How far can a 2×6 purlin on a 6:12 sloped roof span?”
 The following describes 2×6 SYP #2 purlins spanning a 14′ bay, with an on-center spacing of 24″ (sf).
The following describes 2×6 SYP #2 purlins spanning a 14′ bay, with an on-center spacing of 24″ (sf).
Purlins are recessed between rafters with their top edges flush with rafter top edges. Purlins are mounted to rafters with Simpson Strong-Tie LU-26 joist hangers at both ends.
Effective simple beam span length (le) will be taken as 165.
Applied loads
Dead load, D[
Dpurlin: dead load from weight of purlin itself
Dpurlin = purlin density × ((b × d × le) / (sf × l))
Purlin density found via NDS Supplement 2015 Section 3.1.3:
density = 62.4 × (G / (1 + (G × 0.009 × moisture content))) × (1 + (moisture content / 100))
moisture content = 19%
density = 62.4 × (0.55 / (1 + (0.55 × 0.009 × 0.19))) × (1 + (0.19 / 100))
density = 34.56 pcf
Dpurlin = 34.56 pcf × ( ( 1.5″ × 5.5″ × 165″ ) / ( 24″ × 168″ ) ) × 1/12 in/ft
Dpurlin = 0.966 psf
Roof designed for 29g corrugated steel
Dead load from weight of steel (Dsteel) based on values from the American Building Components catalogue:
Dsteel = 0.63 psf
D: dead load
D = Dpurlin + Dsteel
D = 0.966 psf psf + 0.63 psf psf
D = 1.596 psf
Project load to a vector acting perpendicular to the roof plane:
D = D × cos(Θ)
D = 1.596 psf × cos(0.464)
D = 1.428 psf
A conversion from psf to psi will be made for ease of calculation:
D = 1.428 psf × 1/144 psi/psf
D = 0.01 psi
Roof live load, Lr
L: roof live load
Lr = 18 psf
Project load to a vector acting perpendicular to the roof plane:
Lr = Lr × cos(Θ) × cos(Θ)
Lr = 18 psf × cos(0.464) × cos(0.464)
Lr = 14.4 psf
A conversion from psf to psi will be made for ease of calculation:
Lr = 14.4 psf × 1/144 psi/psf
Lr = 0.1 psi
Snow load, S
S: snow load
S = 13.267 psf
Project load to a vector acting perpendicular to the roof plane:
S = S × cos(Θ) × cos(Θ)
S = 13.267 psf × cos(0.464) × cos(0.464)
S = 10.614 psf
A conversion from psf to psi will be made for ease of calculation:
S = 10.614 psf × 1/144 psi/psf
S = 0.074 psi
Wind load, W
W: wind load
W = 9.6 psf
A conversion from psf to psi will be made for ease of calculation:
W = 9.6 psf × 1/144 psi/psf
W = 0.067 psi
Wind uplift load, Wu
Wu: wind uplift load
Wu = -11.763 psf
A conversion from psf to psi will be made for ease of calculation:
Wu = -11.763 psf × 1/144 psi/psf
Wu = -0.082 psi
Lr ≥ S, so roof live loads will dictate in load combinations.
Bending test (fb / Fb′ ≤ 1.0)
Fb: allowable bending pressure
Fb′ = Fb × CD × CM × Ct × CL × CF × Cfu × Ci × Cr
CL = 1
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
CF = 1 NDS Supplement
Ci = 1 NDS 4.3.8
Cr = 1 NDS 4.3.9
S: section modulus
S = (b × d2) / 6
S = (1.5″ × (5.5″)2) / 6
S = 7.563 in3
w: pounds force exerted per linear inch of beam length
M: maximum moment
fb: maximum bending stress
Load combinations:
- D
CD = 0.9
Cfu = 1
Fb′ = 1000 psi × 0.9 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 900 psi
w = (D) × sf
w = 0.008 psi × 24″
w = 0.186 pli
M = (w × l2) / 8
M = ( 0.18559992381479 pli × (165″)2 ) / 8
M = 654.797 in-lbs
fb = M / S
fb = 654.797 in-lbs / 7.563 in3
fb = 86.585 psi
fb / Fb′ ≤ 1.0
86.585 psi / 900 psi ≤ 1.0
0.096 ≤ 1.0
- D + Lr
CD = 1.25
Cfu = 1
Fb′ = 1000 psi × 1.25 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1250 psi
w = (D + Lr) × sf
w = 0.108 psi × 24″
w = 2.586 pli
M = (w × l2) / 8
M = ( 2.5855999238148 pli × (165″)2 ) / 8
M = 9121.997 in-lbs
fb = M / S
fb = 9121.997 in-lbs / 7.563 in3
fb = 1206.214 psi
fb / Fb′ ≤ 1.0
1206.214 psi / 1250 psi ≤ 1.0
0.965 ≤ 1.0
- D + W
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + W) × sf
w = 0.074 psi × 24″
w = 1.786 pli
M = (w × l2) / 8
M = ( 1.7855999238148 pli × (165″)2 ) / 8
M = 6299.597 in-lbs
fb = M / S
fb = 6299.597 in-lbs / 7.563 in3
fb = 833.004 psi
fb / Fb′ ≤ 1.0
833.004 psi / 1600 psi ≤ 1.0
0.521 ≤ 1.0
- D + Wu
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + Wu) × sf
w = -0.074 psi × 24″
w = -1.775 pli
M = (w × l2) / 8
M = ( -1.7748379435325 pli × (165″)2 ) / 8
M = -6261.628 in-lbs
fb = M / S
fb = -6261.628 in-lbs / 7.563 in3
fb = -827.984 psi
fb / Fb′ ≤ 1.0
-827.984 psi / 1600 psi ≤ 1.0
-0.517 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + 0.75Lr + 0.75W) × sf
w = 0.133 psi × 24″
w = 3.186 pli
M = (w × l2) / 8
M = ( 3.1855999238148 pli × (165″)2 ) / 8
M = 11238.797 in-lbs
fb = M / S
fb = 11238.797 in-lbs / 7.563 in3
fb = 1486.122 psi
fb / Fb′ ≤ 1.0
1486.122 psi / 1600 psi ≤ 1.0
0.929 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + 0.75Lr + 0.75Wu) × sf
w = 0.021 psi × 24″
w = 0.515 pli
M = (w × l2) / 8
M = ( 0.51527152330431 pli × (165″)2 ) / 8
M = 1817.878 in-lbs
fb = M / S
fb = 1817.878 in-lbs / 7.563 in3
fb = 240.381 psi
fb / Fb′ ≤ 1.0
240.381 psi / 1600 psi ≤ 1.0
0.15 ≤ 1.0
Purlin stressed in bending to a maximum of 96.5%
Shear test (fv / Fv′ ≤ 1.0)
Fv: allowable shear pressure
Fv′ = Fv × CD × CM × Ct × Ci
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
Ci = 1 NDS 4.3.8
V: max shear force
fv: max shear stress
Load combinations:
- D
CD = 0.9
Fv‘ = 175 psi × 0.9 × 1 × 1 × 1
Fv‘ = 157.5 psi
V = w × (le – (2 × d)) / 2
V = 0.186 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 14.57 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 14.57 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 2.649 psi
fv / Fv′ ≤ 1.0
2.649 psi / 157.5 psi ≤ 1.0
0.017 ≤ 1.0
- D + Lr
CD = 1.25
Fv‘ = 175 psi × 1.25 × 1 × 1 × 1
Fv‘ = 218.75 psi
V = w × (le – (2 × d)) / 2
V = 2.586 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 202.97 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 202.97 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 36.904 psi
fv / Fv′ ≤ 1.0
36.904 psi / 218.75 psi ≤ 1.0
0.169 ≤ 1.0
- D + W
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 1.786 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 140.17 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 140.17 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 25.485 psi
fv / Fv′ ≤ 1.0
25.485 psi / 280 psi ≤ 1.0
0.091 ≤ 1.0
- D + Wu
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = -1.775 pli × ( 165″ – (2 × 5.5″) ) / 2
V = -139.325 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × -139.325 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = -25.332 psi
fv / Fv′ ≤ 1.0
-25.332 psi / 280 psi ≤ 1.0
-0.09 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 3.186 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 250.07 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 250.07 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 45.467 psi
fv / Fv′ ≤ 1.0
45.467 psi / 280 psi ≤ 1.0
0.162 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 0.515 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 40.449 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 40.449 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 7.354 psi
fv / Fv′ ≤ 1.0
7.354 psi / 280 psi ≤ 1.0
0.026 ≤ 1.0
Purlin stressed in shear to a maximum of 16.9%
Deflection test (Δmax / Δallow ≤ 1.0)
I: moment of inertia
I = b × d3 / 12 NDS 3.3.2
I = ( 1.5″ × (5.5″)3 ) / 12
I = 20.797 in4
E: modulus of elasticity
E′ = E × CD × CM × Ct × Ci
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
Ci = 1 NDS 4.3.8
Δallow: allowable deflection
Δmax: maximum deflection
Load combinations:
- D + Lr
CD = 1.25
E′ = 1400000 × 1.25 × 1 × 1 × 1
E′ = 1750000 psi
Per IBC 1604.3 footnote d, dead load may be taken as 0.5D.
w = ((0.5 × D) + Lr) × sf
w = ( (0.5 × 0.01 psi) + 0.1 psi ) × 24″
w = 0.104 pli
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 2.493 pli × (165″)4 ) / ( 384 × 1750000 psi × 20.797 in4 )
Δmax = 0.661″
Δmax / Δallow ≤ 1.0
0.661″ / 1.1″ ≤ 1.0
0.601 ≤ 1.0
- D + W
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 1.786 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.37″
Δmax / Δallow ≤ 1.0
0.37″ / 1.1″ ≤ 1.0
0.336 ≤ 1.0
- D + Wu
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × -1.775 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = -0.368″
Δmax / Δallow ≤ 1.0
-0.368″ / 1.1″ ≤ 1.0
-0.334 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 3.186 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.66″
Δmax / Δallow ≤ 1.0
0.66″ / 1.1″ ≤ 1.0
0.6 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 0.515 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.107″
Δmax / Δallow ≤ 1.0
0.107″ / 1.1″ ≤ 1.0
0.097 ≤ 1.0
Purlin stressed in deflection to a maximum of 60.1%
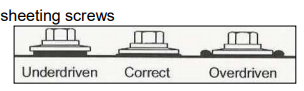 Next possible culprit would be a screw not properly seated. If under driven, (EPDM gasket not compressed) screw can normally be driven in further. If over driven (gasket smashed) screw should be replaced with either a larger diameter and longer length screw (say #14 x 2″) or by driving a wooden match stick or other slender piece of solid wood into screw hole, then use an originally sized screw back in original hole. If a screw was driven in other than perpendicular to roofing, it may be possible to remove the screw and drive it straight in.
Next possible culprit would be a screw not properly seated. If under driven, (EPDM gasket not compressed) screw can normally be driven in further. If over driven (gasket smashed) screw should be replaced with either a larger diameter and longer length screw (say #14 x 2″) or by driving a wooden match stick or other slender piece of solid wood into screw hole, then use an originally sized screw back in original hole. If a screw was driven in other than perpendicular to roofing, it may be possible to remove the screw and drive it straight in.