Solid-sawn vs. Built-up Column Strength
This article was penned by my personal post-frame engineering mentor Dr. Frank Woeste, P.E. and appeared in Journal of Light Construction online (jlconline.com).
Q. Is a site-built column made with three pressure-treated No. 2 southern pine 2x6s and 1/2-inch plywood spacers added to produce a 5 1/2-by-5 1/2-inch cross-section the structural equivalent of a solid-sawn 6×6 post made of the same material? If not, will laminating the layers together with construction adhesive make the column stronger?
A. Frank Woeste, P.E., professor emeritus at Virginia Tech, responds: The short answer to the first question is no; a solid-sawn column will always be stronger than a free-standing, built-up column made with graded dimensional stock of the same lumber species. But it’s possible that the column can be built so that it is strong enough to function as a structural alternative. Don’t rely on glue, though; while it might help and certainly can’t hurt, there’s no way to determine the structural benefit and assign any meaningful values for a field-glued assembly.
Columns are subject to axial compression from gravity loads (and tension from wind uplift). To find the compressive strength of a built-up column made up of three 2x6s, you can’t just look up the compressive strength of one of the 2x6s and multiply it by three. Instead, there’s a formula in the NDS (National Design Specification for Wood Construction) that can be used to find the column’s allowable compression stress. If the 2x6s are nailed together per the rules (see illustration, below), the reduction factor is 0.6, or a 40% reduction in allowable axial stress. It matters what material you use to build the columns. Fortunately, compared with some species, the design properties of 2×6 southern pine are very good.
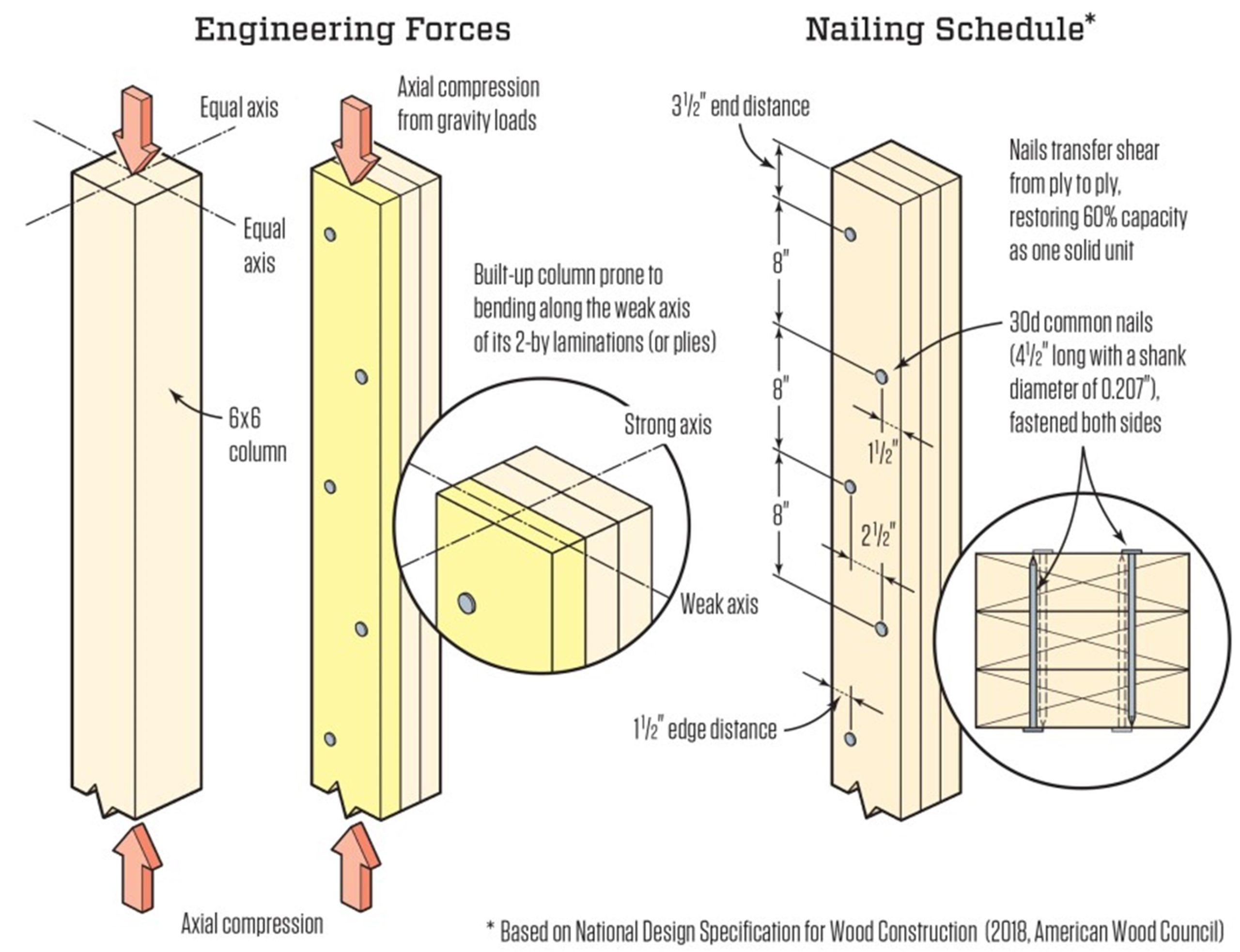
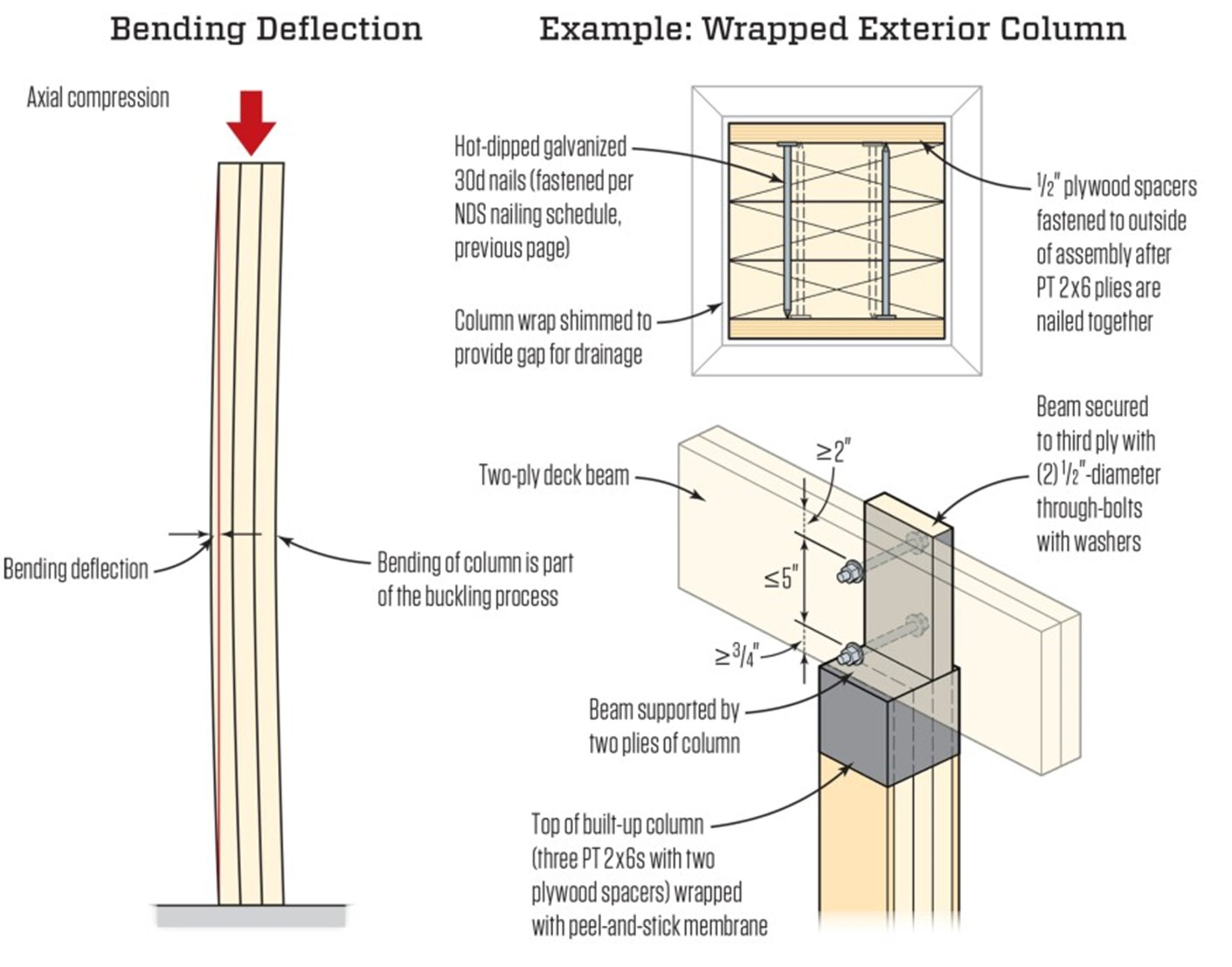
In addition to proper placement, the size and quality of the nails are important. The NDS specifies quality 30d common nails, which have a shank diameter of 0.207 inch and are 4 1/2 inches long, and so will penetrate through all three laminations. As tested, there are no gaps between the 2×6 members of the columns, so any plywood or OSB spacers should be added to the outside of the assembly after the plies are nailed together. It may be possible to fasten the plies together with structural screws, though you would need to determine (likely from their manufacturer) the size and number of screws needed to equal the NDS-required nailing schedule. The purpose of the nails or screws is to transfer shear from ply to ply, as the column is prone to bend about the weak axis. The fastener’s task is to make the plies behave as one solid unit in an attempt to restore some of the bending stiffness and strength that is lost by not using a solid-sawn column.
The overriding principle is “column buckling,” which is the result of “column bending.” “Bending deflection” is the devil. Once an unbraced column starts to bend—let’s call the amount Δ—under an axial load P, a bending moment (P x Δ) is created. This in turn creates more Δ, which creates more bending moment from the same P until eventually the column fails … it’s a runaway process.
In short, there is nothing simple about substituting a three-ply column for a solid-sawn column. Some of the lumber that is now available is much weaker and has lower density, or nail strength, and less stiffness, or modulus of elasticity (E), than southern pine. Along with the design details discussed above, E and compression strength parallel-to-grain are the most important variables for column strength.
“Today I visited the building inspector. I was confirming my intentions of building a Hansen designed structure. The reason is I already have a permit for a building that I was designing and building myself. One of my questions was about snow loads. I explained the layout of roof trusses and purlins on your building design. The inspector asked about the type of wood being used as purlins. I did not know. He gave me a copy of R802.5.1 (3) Rafter spans for common lumber species. The table shows one 2 x 8 that will make a 15ft. span. Is this the code information the inspector should use, or is there something else? What species of lumber is to be used for the purlins?
