Not until reader DON wrote did I realize this information was missing from our Construction Manual (however not any more):
“I’m building a 26×40 pole barn (girts will be nailed to the outside post) and need to finish squaring it up. My square root for the 26×40 is 47.707441767506 and the square root of 25.9×39.9(took3″ off for girts) is 47.56910762248962 Can you tell me what the measurements are in inches after the decimal points? I just want to make sure I’m getting it exact and need a bit of help from someone experienced. Thanks a bunch!”
For those who have not recently utilized their math skills, here is an example: building is 50 feet in width and 84 feet long. Measurements are from outside of column to outside of column, with girts projecting 1-1/2 inches in all directions from column outsides.
Explanation:
A picture helps greatly with this problem, so we begin with a rectangular pole barn.
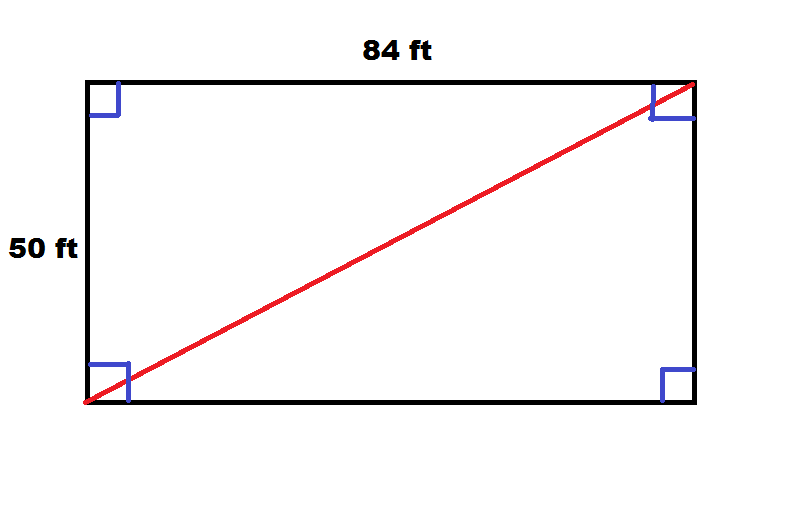
We note distance (drawn in red) is diagonal of our rectangle, or k. We should also note this diagonal divides our rectangle into two congruent right triangles. We can therefore find length of our diagonal by focusing on one of these triangles and determining hypotenuse. This can be done with the Pythagorean Theorem, which gives us:
50^2 + 84^2 = k^2
2500 + 7056 = k^2
9556 = k^2
Taking square root gives us:
k=97.754795 feet
For Don’s building: 26 feet^2 plus 40 feet^2 = 2276
Taking square root of 2276 = 47.707 feet
Less 47 feet leaves 0.707 feet or 8.489 inches (taking decimal of a foot times 12).
0.707 feet – 0.667 feet (eight inches) leaves 0.04 of a foot or ½ inch.
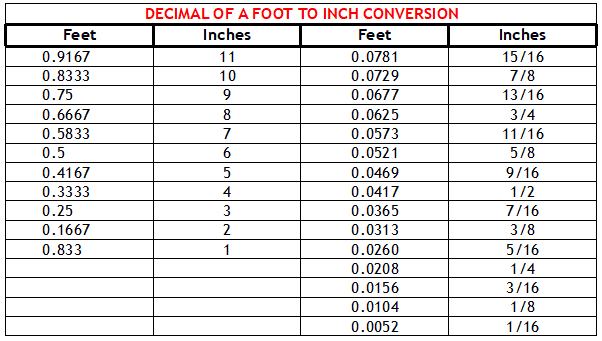
From table above our diagonal is 47’ 8-1/2”.
If, for some reason, corner columns were held in to 25’9” x 39’9” to outsides, then diagonal would be 47’ 4-5/16”.
I hope this helps. Good Luck!